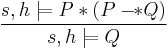Separation logic
In computer science, separation logic[1] is an extension of Hoare logic, a way of reasoning about programs. It was developed by John C. Reynolds, Peter O'Hearn, Samin Ishtiaq and Hongseok Yang,[1][2][3][4] drawing upon early work by Burstall.[5] The assertion language of separation logic is a special case of the logic of bunched implications (BI).[6]
Separation logic facilitates reasoning about:
- programs that manipulate pointer data structures — including information hiding in the presence of pointers;
- "transfer of ownership" (avoidance of semantic frame axioms); and
- virtual separation (modular reasoning) between concurrent modules.
Separation logic supports the developing field of research described by Peter O'Hearn and others as local reasoning, whereby specifications and proofs of a program component mention only the portion of memory used by the component, and not the entire global state of the system. Applications include automated program verification (where an algorithm checks the validity of another algorithm) and automated parallelization of software.
Contents |
Assertions: Operators and semantics
Separation logic assertions describe "states" consisting of a store and a heap, roughly corresponding to the state of local (or stack-allocated) variables and dynamically-allocated objects in common programming languages such as C and Java. A store  is a function mapping variables to values. A heap
is a function mapping variables to values. A heap  is a partial function mapping memory addresses to values. Two heaps
is a partial function mapping memory addresses to values. Two heaps  and
and 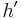 are disjoint (denoted
are disjoint (denoted 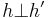 ) if their domains do not overlap (i.e., if for every memory address
) if their domains do not overlap (i.e., if for every memory address 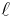 , at least one of
, at least one of 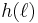 and
and 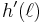 is undefined).
is undefined).
The logic allows to prove judgements of the form 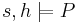 , where
, where  is a store,
is a store,  is a heap, and
is a heap, and  is an assertion over the given store and heap. Separation logic assertions (denoted as
is an assertion over the given store and heap. Separation logic assertions (denoted as  ,
,  ,
,  ) contain the standard boolean connectives and, in addition,
) contain the standard boolean connectives and, in addition, 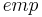 ,
, 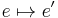 ,
, 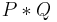 , and
, and 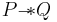 , where
, where  and
and 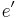 as expressions.
as expressions.
- The constant
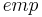 asserts that the heap is empty, i.e.,
asserts that the heap is empty, i.e., 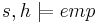 when
when  is undefined for all addresses.
is undefined for all addresses. - The binary operator
 takes an address and a value and asserts that the heap is defined at exactly one location, mapping the given address to the given value. I.e.,
takes an address and a value and asserts that the heap is defined at exactly one location, mapping the given address to the given value. I.e., 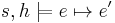 when
when ![h([\![e]\!]_{s}) = [\![e']\!]_{s}](/2012-wikipedia_en_all_nopic_01_2012/I/b30c7e1b3e395b9a2a7854bf8fdb9966.png) (where
(where ![[\![e]\!]_{s}](/2012-wikipedia_en_all_nopic_01_2012/I/45060fdbc2baf53886923a47eb4362ce.png) denotes the value of expression
denotes the value of expression  evaluated in store
evaluated in store  ) and
) and  is otherwise undefined.
is otherwise undefined. - The binary operator
 (pronounced star or separating conjunction) asserts that the heap can be split into two disjoint parts where its two arguments hold, respectively. I.e.,
(pronounced star or separating conjunction) asserts that the heap can be split into two disjoint parts where its two arguments hold, respectively. I.e., 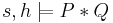 when there exist
when there exist 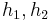 such that
such that 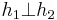 and
and 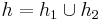 and
and 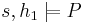 and
and 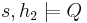 .
. - The binary operator
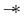 (pronounced magic wand or separating implication) asserts that extending the heap with a disjoint part that satisfies its first argument results in a heap that satisfies its second argument. I.e,.
(pronounced magic wand or separating implication) asserts that extending the heap with a disjoint part that satisfies its first argument results in a heap that satisfies its second argument. I.e,. 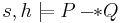 when for any heap
when for any heap 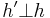 such that
such that 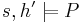 , we also have
, we also have 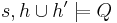 .
.
The operators  and
and 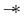 share some properties in common with the classical conjunction and implication operators. They can be combined using an inference rule similar to modus ponens
share some properties in common with the classical conjunction and implication operators. They can be combined using an inference rule similar to modus ponens
and they form an adjunction, i.e., 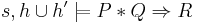 if and only if
if and only if 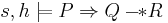 for
for 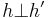 ; more precisely, the adjoint operators are
; more precisely, the adjoint operators are 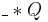 and
and 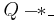 .
.
Reasoning about programs: triples & proof rules
In separation logic, Hoare triples have a slightly different meaning than in Hoare logic. The triple 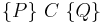 asserts that if the program,
asserts that if the program,  , executes from an initial state satisfying the precondition,
, executes from an initial state satisfying the precondition,  , then the program will not go wrong (e.g., have undefined behaviour), and if it terminates, then the final state will satisfy the postcondition,
, then the program will not go wrong (e.g., have undefined behaviour), and if it terminates, then the final state will satisfy the postcondition,  . In essence, during its execution,
. In essence, during its execution,  may access only memory locations whose existence is asserted in the precondition or that have been allocated by
may access only memory locations whose existence is asserted in the precondition or that have been allocated by  itself.
itself.
In addition to the standard rules from Hoare logic, separation logic supports the following very important rule:
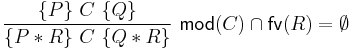
This is known as the frame rule and enables local reasoning. It says that a program that executes safely in a small state (satisfying  ), can also execute in any bigger state (satisfying
), can also execute in any bigger state (satisfying  ) and that its execution will not affect the additional part of the state (and so
) and that its execution will not affect the additional part of the state (and so  will remain true in the postcondition).
will remain true in the postcondition).
Implementations
The Ynot library for the Coq proof assistant contains an implementation.
References
- ^ a b Separation Logic: A Logic for Shared Mutable Data Structures. John C. Reynolds. LICS 2002.
- ^ Intuitionistic Reasoning about Shared Mutable Data Structure. John Reynolds. Millennial Perspectives in Computer Science, Proceedings of the 1999 Oxford-Microsoft Symposium in Honour of Sir Tony Hoare
- ^ BI as an Assertion Language for Mutable Data Structures. Samin Ishtiaq, Peter O'Hearn. POPL 2001.
- ^ Local Reasoning about Programs that Alter Data Structures. Peter O'Hearn, John Reynolds, Hongseok Yang. CSL 2001
- ^ Some techniques for proving programs which alter data structures. R.M. Burstall. Machine Intelligence 7, 1972.
- ^ The Logic of Bunched Implications P.W. O'Hearn and D. J. Pym. Bulletin of Symbolic Logic , 5(2), June 1999, pp215-244